Three Words I'm Eliminating from my Math Vocabulary
Before we begin, take a moment and read the number sentence below out loud. Don't think about it too much, just read it as you normally would to a class or colleague.
Over time, many of us adopt "shortcuts" when it comes to talking about the symbolic representation of mathematics. We may know what we mean to say, but for students who struggle, the meanings of these shortcuts are not always apparent, and might even cause confusion.
The following are three very small, deliberate changes in language I am trying to work into my practice moving forward. Though each is a simple change, I'm having a hard time undoing decades of bad habits!
As a result, with some classes we worked this past year, up to half of the students placed the number "12" in the box below, thinking that "the answer goes after the equals sign:"
To counter this, and to reinforce the idea of balance in an equation, I am trying to stop saying "equals" when reading a number sentence.
Instead of reading "3 + 4 = 7" as "three plus four equals seven," say "three plus four is the same as seven" or "three plus four is equivalent to seven."
Mike posits that one possible reason for this is that we, as adults, have become so accustomed to pronouncing the number 401 as "four-oh-one." For a student who struggles with sense of number and counting, it might make sense that a four-oh-nine would be followed by a four-oh-ten.
Even though we as teachers know what we mean by the "oh," many of us have come to assume that all students know what we mean as well. Students have become good at hiding what they don't understand. By using the right language, we can not only help struggling students, but also reinforce good habits in their language.
Instead of reading "308" as "three-oh-eight," say "three hundred, eight" or "three hundred and eight."
SO many students struggle with what a fraction represents, and how to visualize a fraction, that we do them a huge disservice by just reading a fraction as separate and individual numbers. Just as "two beside three" obliterates the meaning of two tens and three ones, "one over three" removes all meaning of one third.
Instead of reading 3/5 as "three over five," say "three fifths" or, even better, "three one-fifths."
How did you read this number sentence at the beginning of the post? Did you say "equals," "oh," or "over?" What other language shortcuts do we often fall into?
On Language
This past year, I have been doing more work in looking at how aspects of literacy creep into (and affect) how we teach and learn math. One theme that reoccured in different contexts was language, and paying close attention to what we say when we are teaching math.Over time, many of us adopt "shortcuts" when it comes to talking about the symbolic representation of mathematics. We may know what we mean to say, but for students who struggle, the meanings of these shortcuts are not always apparent, and might even cause confusion.
The following are three very small, deliberate changes in language I am trying to work into my practice moving forward. Though each is a simple change, I'm having a hard time undoing decades of bad habits!
"Equals"
Based on some of our work on equivalence this past year with grade 7-9 students (which was based on the work of Carpenter et al. (2003)), we saw that many students have started equating (to pardon the pun) the equals sign with "find the answer;" it's what you hit on the calculator in order to give you the solution. For many, it no longer represents a balance or equivalence to be maintained.As a result, with some classes we worked this past year, up to half of the students placed the number "12" in the box below, thinking that "the answer goes after the equals sign:"
To counter this, and to reinforce the idea of balance in an equation, I am trying to stop saying "equals" when reading a number sentence.
Instead of reading "3 + 4 = 7" as "three plus four equals seven," say "three plus four is the same as seven" or "three plus four is equivalent to seven."
"Oh"
Mike Jacobs (@msbjacobs) presented a fascinating talk at OAME2019 this past spring, which in part spoke to how students' trouble with counting can impact much higher mathematical function. On one diagnostic, it was interesting to see some grade 9 students incorrectly continue a series as follows:
106, 107, 108, 109, 1010, 1011, 1012...
Mike posits that one possible reason for this is that we, as adults, have become so accustomed to pronouncing the number 401 as "four-oh-one." For a student who struggles with sense of number and counting, it might make sense that a four-oh-nine would be followed by a four-oh-ten.
Even though we as teachers know what we mean by the "oh," many of us have come to assume that all students know what we mean as well. Students have become good at hiding what they don't understand. By using the right language, we can not only help struggling students, but also reinforce good habits in their language.
Instead of reading "308" as "three-oh-eight," say "three hundred, eight" or "three hundred and eight."
"Over"
At a NOMA fractions workshop by Tara Flynn (@taracflynn) and Shelley Yearley (@ShelleyYearley) earlier this year, I remember Shelley relating to the group:SO many students struggle with what a fraction represents, and how to visualize a fraction, that we do them a huge disservice by just reading a fraction as separate and individual numbers. Just as "two beside three" obliterates the meaning of two tens and three ones, "one over three" removes all meaning of one third.
Instead of reading 3/5 as "three over five," say "three fifths" or, even better, "three one-fifths."
How did you read this number sentence at the beginning of the post? Did you say "equals," "oh," or "over?" What other language shortcuts do we often fall into?
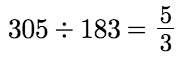





I'm not American, so I read "three hundred five divided by one hundred eighty-three is equal to five divided by three". I agree, the way we say mathematical sentences affects students' understanding. But I don't think "is the same as" will make them see further from the blank in 4+8=_+5. I'm trying to introduce algebraic language saying "five times x" for 5x, and so on. I also say "adding 3 both sides" for any operation done to equations. Maybe you should start a list in gsheets to include more words at different levels!!!
ReplyDeleteI would also comment that sometimes is useful to read 3/5 as three divided by five, instead of three one-fifths, for example, to explain the division of fractions.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteI thought the last two examples in particular were effective, as I can think of quite a few times I use the same words for three digit numbers and for fractions. It's also a great point you brought up, about how the shortcuts that are evident to math teachers might not be as clear to students. With the first example, it seems like that relates less to using accurate language as it does to prior conceptions students have when introduced to some algebraic concepts, though I think it could be valuable to also use words like "equivalent to" to reinforce what it means for two expressions to be on opposite sides of the equals sign
ReplyDelete